합성함수 미분 쉽게 푸는 법

합성함수 미분 쉽게 푸는 법

오늘도 미분하느라 고통 받는 이과 횐님들, 잘 지내셨나영?? 오늘은 이과 횐님들에게 꼭 필요한 합성함수 미분법을 총정리할 거예영. 합성함수 미분 헷갈리시면 수능 때 눈물 펑펑이라구욧! 하지만 우리 횐님들은 1초컷 하실 수 있으실 거예영. 그럼 미분하러 출~바알!😄

 

합성함수 미분 쉽게 푸는 법

합성함수 넘나 어려운 것.ㅠㅠㅠ 1학년 때도 어려웠는데, 이제 우리는 이 아이들을 미분해야 합니다. 우선 합성함수를 미분하기 전에영, 합성함수가 무엇인지 떠올려 봅시다~~~ 합성함수는 y=(cosx)²처럼 함수 속에 함수가 또 들어가 있는 꼴을 말해영. 함수가 1개인데 어디에 들어가 있냐고 하시겠지만, 이 함수는 y=t²의 t 자리에 cosx가 들어가 있는 모양이라고 볼 수 있어영. 즉, 이차함수와 삼각함수가 합성된 꼴인 것이에영. 이러한 아이들은 우리가 외운 공식에 나와있지 않으므로 합성함수의 미분법을 활용합니다.

 

교과서에는 연쇄법칙(chain rule)이나 속미분 등으로 표현이 되어 있을 텐데영, 우리는 핵심 스킬을 익혀봅시다. 비법은영!!

합성돼 있는 함수를 □로 치환하면 됩니다

예를 들어 볼게영. y=(cosx)²이라는 함수에서 cosx=□로 치환해서 y=□²이라고 생각하고 미분을 하는 것이에영! 그러면 수학2에서 배웠듯이 y'=2□가 됩니다. 그런데 여기서 끝이 아니고영!! 뒤에 □'을 꼭 붙여주셔야 해영. 이 아이를 속미분이라고 하지영. 즉, y'=2□×□'이 되고영, □에 cosx를 대입해 주면, y'=2(cosx)×(-sinx)=-2cosxsinx가 됩니다.

 

그럼 함수의 종류별로 살펴보도록 해영.

 

1) 지수함수

지수함수는 문제에서 준 지수함수를 그대로 베끼고영(밑이 a일 경우 lna 붙여야 함), 지수를 미분한 아이를 뒤에 붙여 주면 됩니다. 예를 들어, y=e^(x²)을 미분한다고 하면, 우선 y'=e^(x²)라고 쓰고, 지수에 있는 x²을 미분한 2x를 붙여주라는 것이졍. 그래서 최종 답은 y=2xe^(x²)이 됩니다. 만약 y=2^(x²)를 미분한다면 y'=2^(x²)×ln2를 쓴 뒤에 2x를 붙여주세영. 따라서 y'=2^(x²)×ln2×2x입니다~~ 참 쉽졍?

 

2) 로그함수

로그함수는 더 쉬워영. 진수에 있는 문자를 분모에 그대로 베끼고(밑이 a일 경우 1/lna 붙여야 함), 진수를 미분한 아이를 분자에 써 주면 돼영. 예를 들어, y=ln(x²+3)을 미분한다고 하면 우선 y'=1/(x²+3)이라고 쓴 뒤, 분자에 x²+3을 미분한 2x를 쓰시면 됩니다. 즉 y'=(2x)/(x²+3)이 됩니다. 이 아이는 나중에 적분에서 엄청 나오기 때문에 꼭!!! 암기하시고 익숙해져야 해영.

 

3) 삼각함수

삼각함수는 조금 어려울 수 있는데영, 함수의 종류에 따라 미분이 다 다르기 때문이에영. 삼각함수의 미분 때문에 고통받는 횐님들은 이 글을 보고 암기하고 오시면 도움이 될 거예영. 공식을 다 암기하셨다는 가정 하에 설명을 해 볼게영.

 

이 아이는 웬만하면 치환을 해서 푸시는 걸 추천해영. 삼각함수는 공식을 써서 미분한 뒤 각도 부분에 나오는 함수를 미분한 아이를 한 번 더 붙여주면 됩니다. 예를 들어 y=sin(2x-1)을 미분한다고 하면 y=sin□로 바꾸어서 y'=cos□라고 쓴 다음에 □'을 곱해 주시면 돼영. 그러니까 답은 y'=cos(2x-1)×2=2cos(2x-1)이 됩니다.

 

4) 음함수

마지막으로 음함수예영. 음함수가 왜 여기 들어있냐고 하실 수 있지만, 음함수의 미분은 합성함수의 미분과 꽤 유사합니다. 그래서 한 번에 가르쳐 드리겠어영!!

 

우선 음함수라는 것은 f(x, y)=0꼴로 나타낸 함수를 말해영. 우리가 아는 y=2x도 y-2x=0으로 쓰면 음함수가 되지영. 그런데 우리가 미분하고 싶은 아이들은 원, 포물선, 타원, 쌍곡선처럼 x와 y가 섞여있거나 xⁿ, xy, yⁿ항 등이 들어있어서 y=f(x)로 표현하기 힘든 아이들을 뜻해영. 이런 아이들은 합성함수 미분처럼 풀어주면 1초컷이에영.

 

x²+xy+y²=3이라는 식을 봅시다. 이 식을 미분하라고 하면 dy/dx를 구하라는 뜻이에영. 주어진 식을 x로 미분하라는 거지영. x²은 미분이 가능한데, y²은 x로 미분이 안 되지영? 이럴 때 우선 y²을 y로 미분한 다음에 뒤에 dy/dx를 붙여주면 되는 거예영! 이것이 바로 합성함수의 미분이거든영. 그리고 xy를 미분할 때는 곱함수의 미분법인 미그그미를 활용하면 됩니다. 그러면 이 아이를 미분한 식은 2x+y+xdy/dx+2ydy/dx=0이 되고, 정리해주면 dy/dx=-(2x+y)/(x+2y)입니다. 분모가 0이면 안 되니, (x+2y≠0)을 꼭 써 주세영.

 

 

합성함수 미분법에서 중요한 것은,

① 누구를 치환할 것인가 ② 무슨 문자로 미분하고 있는가

 

예영. 이 두 가지에 유의하면서 풀어보세영!!

 

연습문제를 만들었으니, 한 번 위에서 배운 내용들을 적용해보세영~~

 

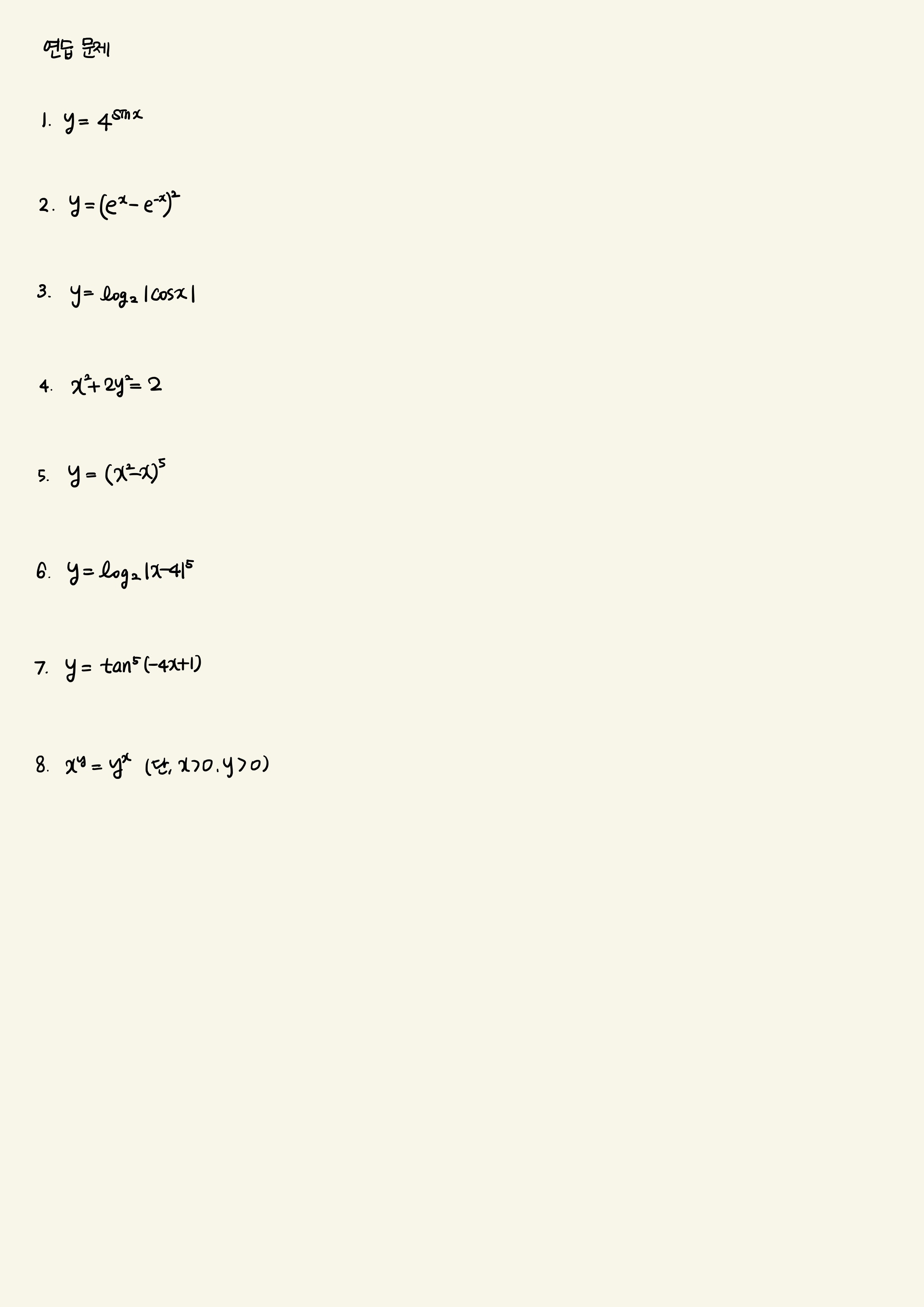
합성함수 미분 쉽게 푸는 법 연습 문제

 

문제 다 풀고 스크롤해 주세영~~ (답 있음)

 

답은 이렇습니다.

합성함수 미분 쉽게 푸는 법 연습 문제 답

7번 문제는 2번 합성돼 있는 아이라서, □로 치환한 뒤 △로 또 치환했어영. 이걸 굉장히 어려워하시더라고영. 정말 어려운 문제들은 3, 4번 치환해야 할 때도 있어영. 이런 문제를 잘 풀려면 연습뿐이겠졍.ㅠ

 

8번 문제는 다항함수꼴도 아니고 지수함수 꼴도 아닌, 양변에 ln을 씌워서 미분해야 하는 문제예영.

 

다항함수: y=xⁿ꼴 (밑이 변수)
지수함수: y=a^x꼴 (지수가 변수)
양변에 ln 취해야 풀리는 함수: y=x^x (밑과 지수가 모두 변수)

 

양변에 ln을 취하고 나서도 y를 미분할 때는 끝까지 집중을 해야 정답을 맞힐 수 있겠졍? 이과 미분 넘나 어려운 것.ㅠ 오늘 좀 어려웠네영. 하지만 횐님들은 잘하실 수 있을 거예영.

 

 

시그마 공식도 부숴보세영! 🦄

시그마 공식 부수기 (ΣK, ΣK², ΣK³)